Fibonacci
Tá Fibonacci ar dhuine de na matamaiticeoirí Eorpacha is tábhachtaí a mhair riamh. Bhí sé beo le linn na meánaoiseanna. Deirtear gurb é a thug córas nua-aimseartha uimhreacha isteach san Eoraip agus gur chuidigh sé linn foghlaim faoi sheichimh uimhreacha.
Dealbh de Leonardo Fibonacci a críochnaíodh in 1863 in Camposanto di Pisa – reilig chlúiteach in Pisa, an Iodáil
(Pic le Hans-Peter Postel)
Cérbh é Fibonacci?
Rugadh Fibonacci sa bhliain 1170 i mbaile darb ainm Pisa. Tá Pisa suite san Iodáil sa lá atá inniu ann, ach is tír measartha nua í an Iodáil. Ní raibh tír darbh an Iodáil ann ar chor ar bith nuair a rugadh Fibonacci.
Rud eile, ní ‘Fibonacci’ an fíorainm a bhí air go fiú. Leonardo Bonacci an t-ainm a bhí air. Is cineál de leasainm é Fibonacci. Tháinig sé ó filius Bonacci – rud a chiallaíonn ‘mac Fibonacci’.
Ach, ní bheadh sé míchothrom a rá gurbh é Fibonacci a chuir ar a súile do na tíortha in iarthar an domhain cé chomh tábhachtach is a bhí an mhata.
Tá clú ar bhaile Pisa mar gheall ar an Túr Claonta atá ann
(Pic le Yair Haklai)
Cúlra
Nuair a deir muid ‘an tIarthar’ is é atá i gceist againn ná Iarthar na hEorpa – an Bhreatain, an Fhrainc, an Ísiltír, an Ghearmáin, an Spáinn agus an Iodáil sa lá atá inniu ann. Caithfidh muid a chuimhneamh nach raibh na hainmneacha sin orthu mar thíortha sa bhliain 1170.
An fáth nach bhfuil Meiriceá luaite mar chuid den Iarthar ná nach raibh a fhios ag muintir na hEorpa ag an am sin go raibh Meiriceá ann. Shíl siad go raibh an domhan cothrom agus, dá rachfá rófhada amach ó chósta Mhaigh Eo – go dtitfeá de dhroim an domhain!
Nuair a smaoinímid ar ‘an Iarthar’ sa lá atá inniu ann, smaoinímid ar na tíortha is saibhre agus is forbartha agus is sibhialta ar domhan. Tá an teicneolaíocht is úire againn, tá an eolaíocht is fearr againn. Ach ní mar sin i gcónaí a bhí an scéal.
Le linn na meánaoiseanna, ní raibh an Eoraip chomh forbartha sin ná chomh sibhialta sin ar chor ar bith. Ainm eile a thugtar ar na meánaoiseanna ná an Ré Dhorcha. Tugtar ‘an Ré Dhorcha’ ar an tréimhse míle bliain idir titim Impireacht na Róimhe agus Aimsir an Renaissance mar nár tharla mórán dul chun cinn ná foghlama san Eoraip le linn an ama seo.
Nuair a thit Impireacht na Rómhánach, ní raibh a oiread sin dul chun cinn ann san Eoraip ó thaobh na heolaíochta ná na teicneolaíochta de ar feadh tréimhse fhada
(Músaem Chicago)
Bhí clú ar na Rómhánaigh as cé chomh forbartha agus cé chomh sibhialta is a bhí an tsochaí s'acu. Ach i ndiaidh d'Impireacht na Róimhe titim as a chéile, ní dhearna an Eoraip mórán dul chun cinn eile ar chor ar bith - go háirithe sa mhatamaitic - ach d’athraigh Fibonacci sin.
An Mhatamaitic sna meánaoiseanna
Ceann de na míbhuntáistí is mó a bhí ag an Eoraip ó thaobh na matamaitice de ná go raibh seanchóras uimhreacha na Rómhánach go fóill in úsáid acu. Cuimhnigh nár bhog rudaí ar aghaidh mórán ó bhí aimsir na Rómhánach ann.
Bhí na huimhreacha Rómhánacha go breá le rudaí simplí a chuntas, airgead, mar shampla, nó le taifead a choinneáil de bhlianta. Ach ní raibh na huimhreacha Rómhánacha rómhaith má bhí tú ag iarraidh suimeanna nó mata níos casta a dhéanamh.
Ní raibh rud ar bith ag na Rómhánaigh, go fiú, a sheas don uimhir náid. An rud nach raibh ar eolas ag cuid mhór daoine san Eoraip ag an am seo ná go raibh córais uimhreacha in úsáid in áiteanna eile ar domhan a bhí i bhfad níos fearr ná córas na Rómhánach.
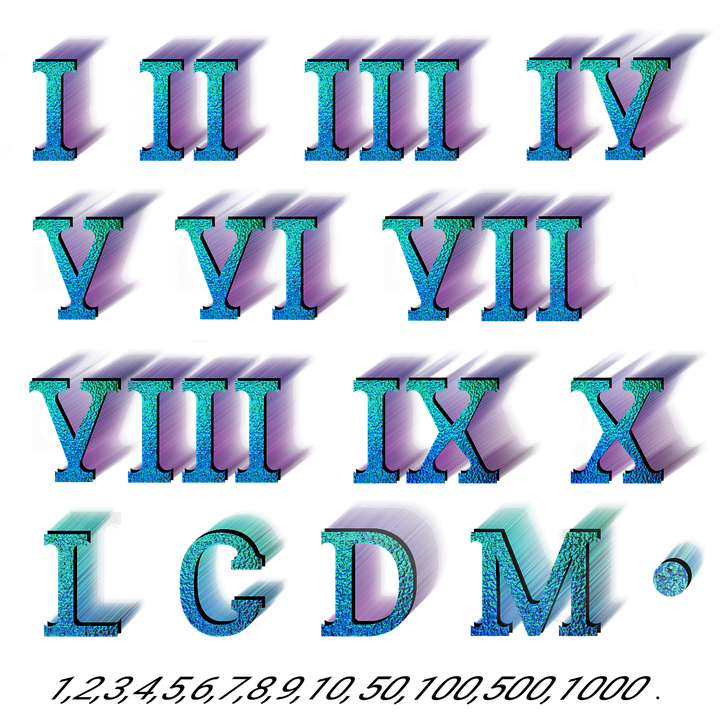Na huimhreacha Rómhánacha
Córais Uimhreacha Eile
Smaoinigh ar na huimhreacha atá againn sa lá atá inniu ann “ár gcuid uimhreacha”.
0, 1, 2, 3, 4, 5, 6, 7, 8, 9.
Le fírinne – ní linne iad. Fuair muid ar iasacht iad. Tá an córas seo uimhreacha bunaithe ar chóras a tháinig as India - an Córas Hiondúch Uimhreacha. Tháinig matamaiticeoirí ón India aníos leis an chóras seo idir an 1ú agus an 4ú céad AD. Ansin, spréigh sé chuig tíortha Arabacha, ach gur athraigh siad féin é rud beag.
Sa lá atá inniu ann, tugaimid an Córas Hiond-Arabach air. Bhí sé i bhfad níos éifeachtaí ná an córas a bhí ag na Rómhánaigh.
Caithfidh muid an chuid is mó den bhuíochas a ghabháil le Fibonacci as córas seo na n-uimhreacha a thabhairt isteach san Eoraip.
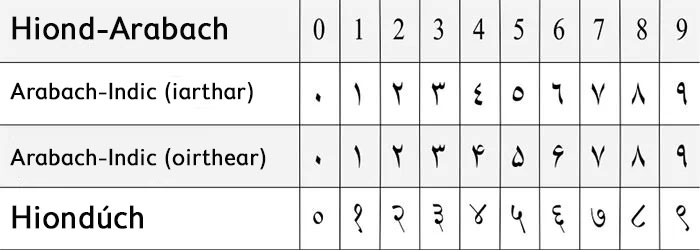Caithfidh muid buíochas a ghabháil le Fibonacci as an chóras uimhreacha a úsáidimid sa lá atá inniu ann a thabhairt dúinn
Óige Fibonacci
Guglielmo an t-ainm a bhí ar athair Fibonacci. Is ceannaí iontach saibhir a bhí ann. Rinne sé a lán trádála leis an Afraic agus chaith sé cuid mhór ama san Afraic. Gach áit a ndeachaigh sé, chuaigh Fibonacci leis. Mar sin de, chaith Fibonacci cuid mhór ama i dtuaisceart na hAfraice nuair a bhí sé óg. Chaith sé a lán ama le ceannaithe ón Afraic agus ón Mheán-Oirthear agus d’fhoghlaim cuid mhór rudaí uathu faoi uimhreacha agus an dóigh a ndearna siadsan cuntas.
Bhí suim i gcónaí ag Fibonacci sna huimhreacha agus sa mhatamaitic. Nuair a bhí sé níos sine, scríobh Fibonacci leabhar matamaitice agus rinne sé seo athrú mór ar an dóigh a ndéanaimid matamaitic san Eoraip.
Liber Abaci (Leabhar an Áirimh)
Sa bhliain 1202, scríobh Fibonacci leabhar darbh ainm Liber Abaci. Ciallaíonn teideal an leabhair ‘leabhar an áirimh’ nó, níos simplí, ‘leabhar a léiríonn do dhaoine an dóigh le suimeanna a dhéanamh.
Leathanach as Liber Abaci
Scríobh sé sa leabhar faoi Chóras Hiond-Arabach na n-uimhreacha (le feiceáil thuas) agus faoin dóigh le suimiú, dealú, iolrú agus roinnt a dhéanamh. Na rialacha ar chuir Fibonacci síos orthu – úsáidimid a bheag nó a mhór na rialacha ceannann céanna sa lá atá inniu ann.
Ní raibh an mhata furasta leis na huimhreacha Rómhánacha.
Mar shampla,
CLXXIIII + XXVIII = CCII
CLXXIIII – XXVIII = CXXXXVI
Sna huimhreacha Rómhánacha a fhoghlaimíonn muidne, bíonn ord na litreacha tábhachtach.
Mar shampla, MMIII = 2003
Ach bhí rud eile iontach suimiúil sa leabhar seo. Rinne Fibonacci fiosrú ar uimhreacha agus rinne sé iarracht patrúin a aimsiú sna huimhreacha.
Tugaimid ‘seicheamh’ ar liosta uimhreacha a bhfuil patrún ann a cheanglaíonn iad. Tá staraithe measartha cinnte nach raibh Fibonacci ar an chéad duine riamh le patrúin agus seichimh uimhreacha a fhiosrú ach aontaíonn a lán daoine gur dhírigh sé aird daoine ar an mhatamaitic – go háirithe san Eoraip.
Uimhreacha Fibonacci
An rud is clúití i leabhar Fibonacci ná an rud a dtugaimid ‘uimhreacha Fibonacci’ orthu. Is seicheamh uimhreacha iad a thug Fibonacci faoi deara. I gcaibidil a 12 den leabhar, chuir sé ceist iontach clúiteach faoi choiníní.
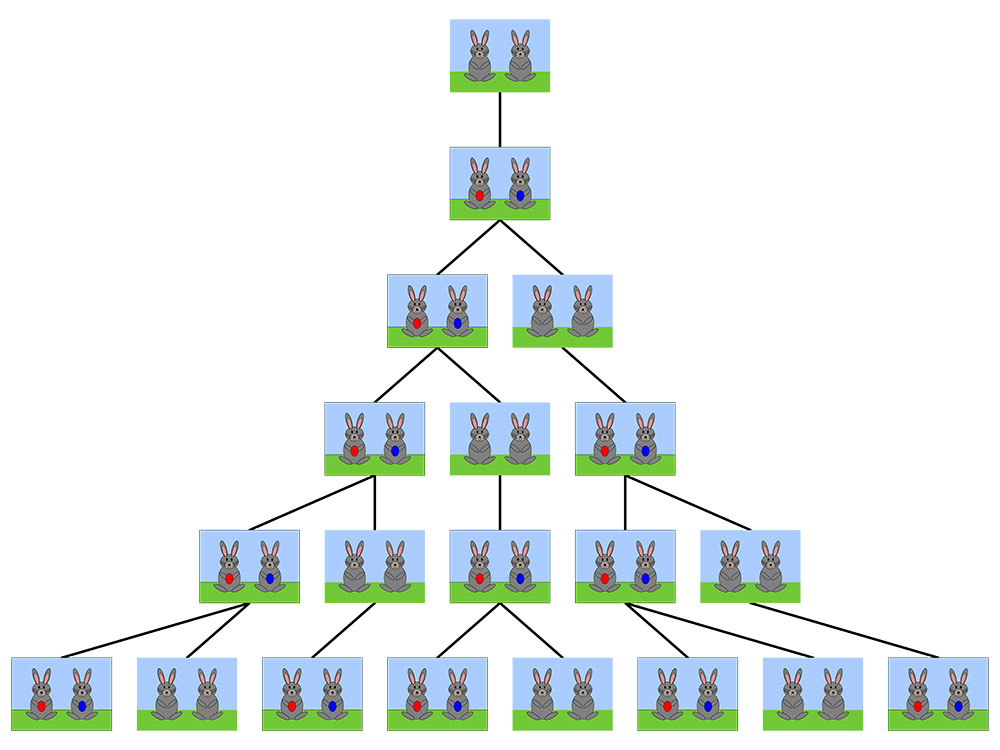Chuir Fibonacci ceist iontach clúiteach faoi choiníní agus é ag smaoineamh ar an dóigh a dtiocfadh fás ar phobal coiníní
(Íomhá le Michael Frey)
Ní fiú dul isteach i gceist na gcoiníní anseo ach is fiú go mór amharc ar an seicheamh uimhreacha ar tháinig Fibonacci aníos leis.
Sa seicheamh seo, faighimid an chéad uimhir eile tríd an dá uimhir roimpi a shuimiú le chéile.
Téann an seicheamh seo ar aghaidh agus ar aghaidh agus ar aghaidh gan stad.
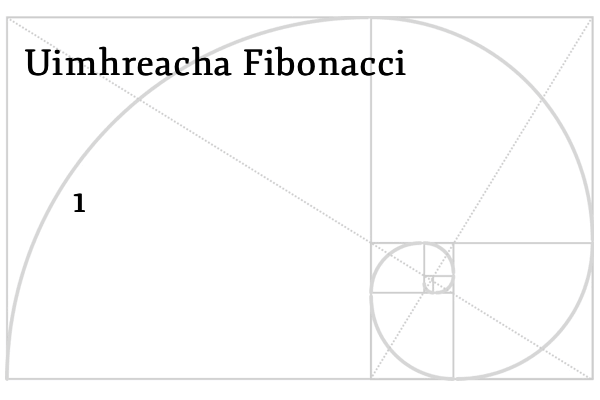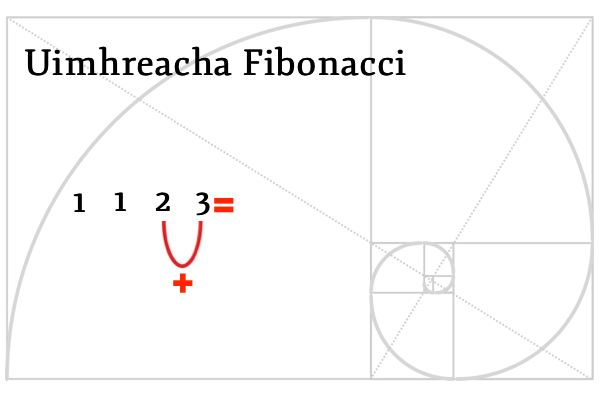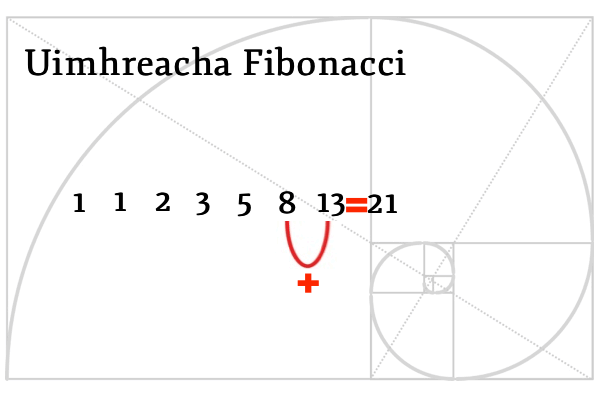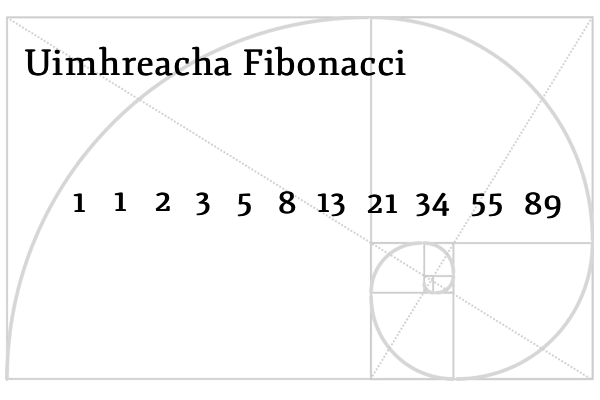An seicheamh ar tháinig Fibonacci aníos leis – Uimhreacha Fibonacci
Suimiúil go leor, dar leat? Ach tá go leor seicheamh eile uimhreacha ann a théann ar aghaidh gan stad. Cad é atá chomh speisialta sin faoi Uimhreacha Fibonacci?
Bhuel, ní hé gur patrún randamach iad uimhreacha Fibonacci - is patrún iontach speisialta iad. Patrún atá le feiceáil i gcuid mhaith áiteanna thart timpeall orainn.
Uimhreacha Fibonacci sa nádúr
In amanna, nuair a amharcaimid ar chruthanna sa nádúr, sílimid gur cruthanna randamacha iad ach má dhéanaimid scrúdú rud beag níos géire orthu - tchífidh muid nach bhfuil siad chomh randamach sin ar chor ar bith.
Uimhreacha Fibonacci agus bláthanna – déan cuntas ar líon na bpeiteal i ngach sraith, an bhfuil patrún sna huimhreacha le tabhairt faoi deara? (Pic le hAlvegaspar)
Go fiú i lár an bhlátha – tá patrúin Fibonacci le sonrú (RD Bury a chuir in oiriúint)
Tógaimis bláthanna, mar shampla. An chéad bhláth eile a fheicfidh tú, cuntais líon na bpeiteal air – is mór an seans gur uimhir Fibonacci é.
Nuair a fhásann planda nó crann rud beag níos mó, fásfaidh níos mó gas air. Cuntais líon na ngas - tchífidh tú gur uimhir Fibonacci é.
Tá patrún uimhreacha Fibonacci le feiceáil ar phlandaí cuid mhaith fosta…
…agus go fiú ar anainn!
An Cóimheas Órga agus an Bhís Órga
Tá ceangal eile idir uimhreacha Fibonacci agus an saol atá thart timpeall orainn. Má ghlacaimid dhá cheann ar bith de na huimhreacha Fibonacci a thagann go díreach i ndiaidh a chéile, thig linn an ceann is mó a roinnt ar an cheann is lú leis an ‘chóimheas órga’ a fháil. Cuidíonn an cóimheas órga linn uimhreacha Fibonacci a oibriú amach.
B'fhéidir nár aithin tú é riamh, ach tá an cóimheas órga (an dóigh a mbíonn uimhreacha Fibonacci gaolta lena chéile) le feiceáil i gcuid mhaith de na cruthanna atá thart timpeall orainn. Cruthanna sa nádúr agus cruthanna nach bhfuil chomh nádúrtha sin.
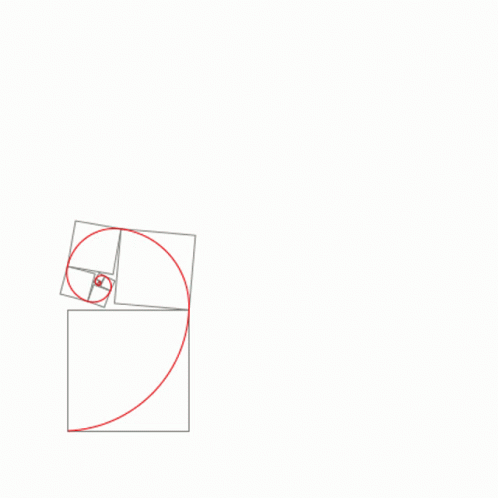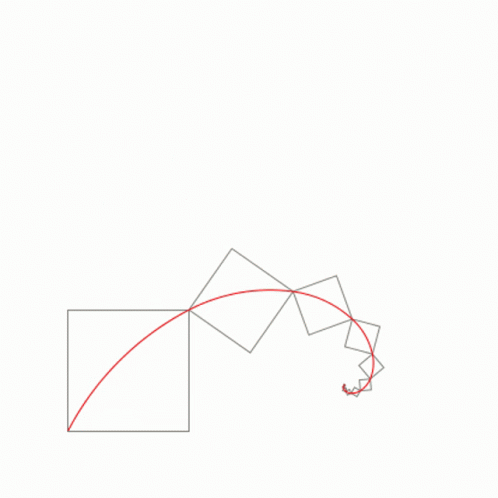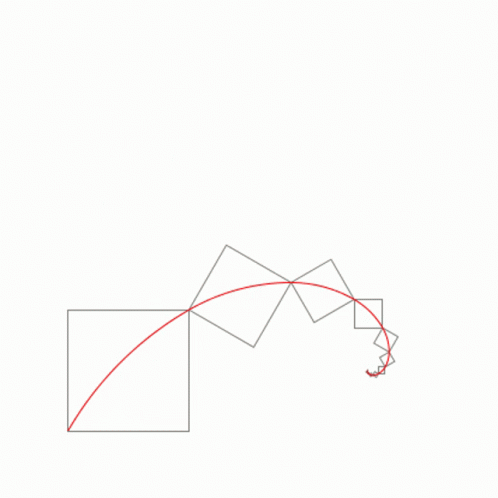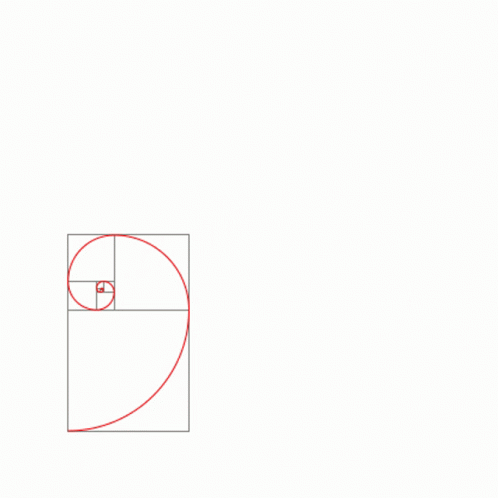
Déanann sleasa na gcearnóg seo uimhreacha Fibonacci - amharc an cruth a dhéanann siad nuair a chuirtear le chéile iad (tenor.com)
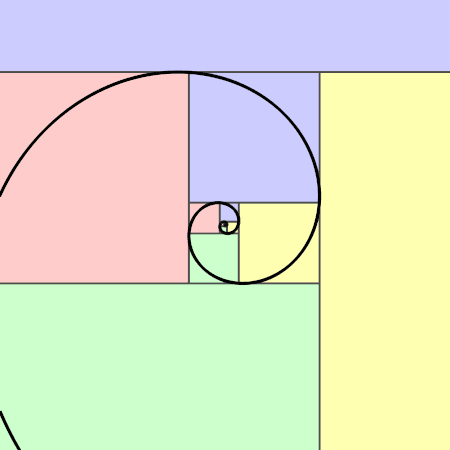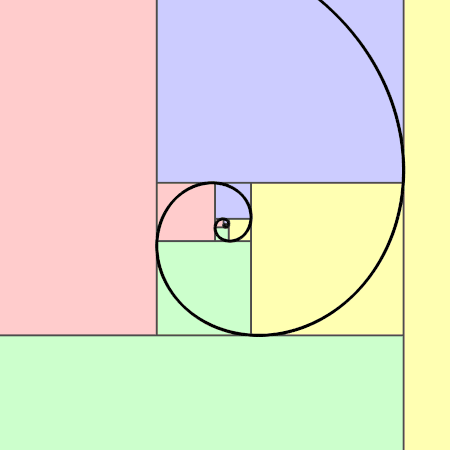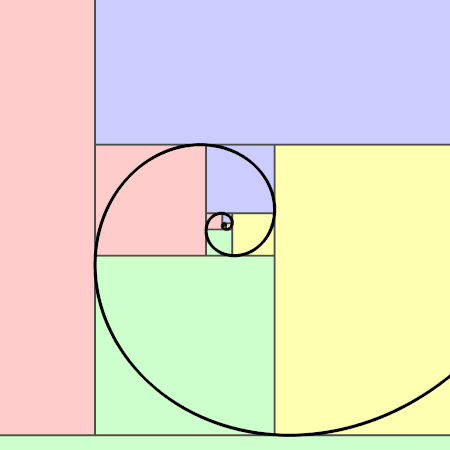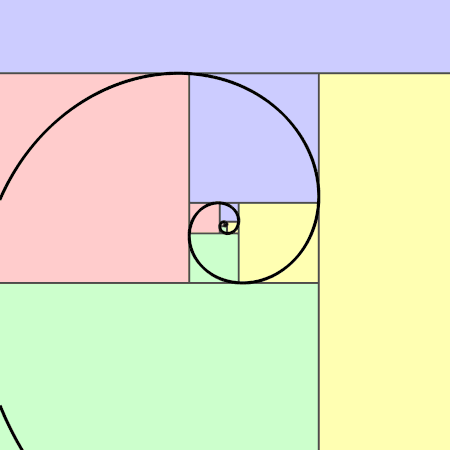
Is seicheamh iad uimhreacha Fibonacci a théann ar aghaidh gan stad (pic: Jahobr)
Amharc ar na cearnóga thuas. Is cearnóg í gach ceann acu de cheann de na hUimhreacha Fibonacci. Má amharcaimid ar chuid mhaith de na foirgnimh is clúití ar domhan, is léir go bhfuil cosúlacht idir iad agus na cearnóga seo. Níl a fhios againn an ndearnadh seo d'aon turas nó an comhtharlú é ach tá an cóimheas órga le sonrú i gcuid mhór acu (mar shampla, má roinneann tú cuid de na faid sna foirgnimh seo ar a chéile – faigheann tú an cóimheas órga).
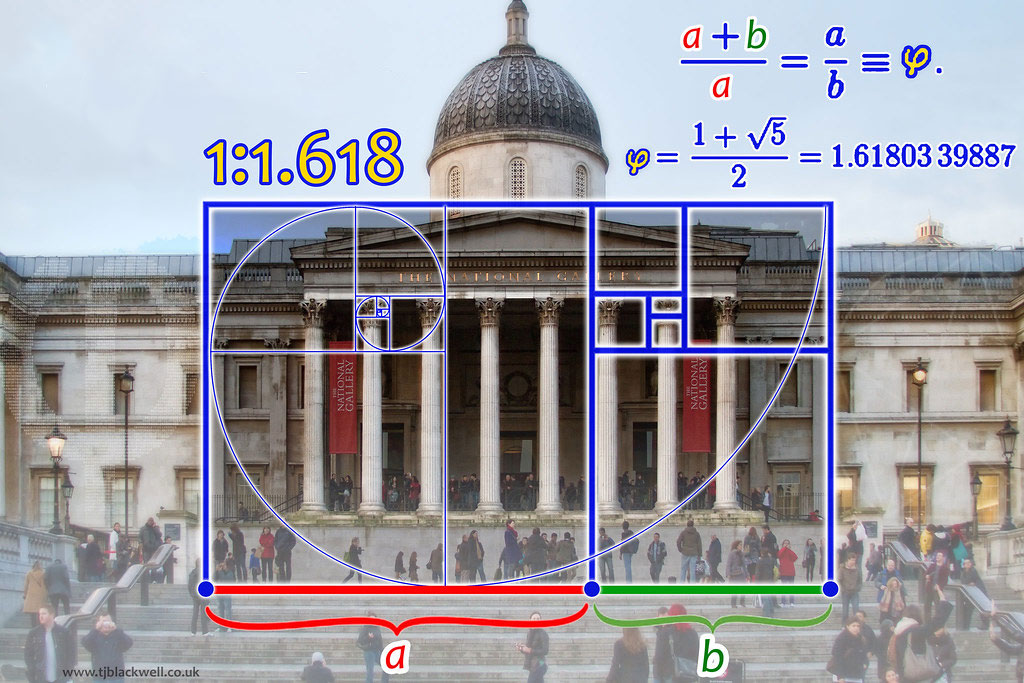
Uimhreacha Fibonacci san ailtireacht… (Pic le Tom Blackwell)
Mar an gcéanna, san ealaín agus sa ghrianghrafadóireacht, bíonn go leor pictiúr agus cruthanna atá bunaithe ar an chóimheas órga. Cén fáth?
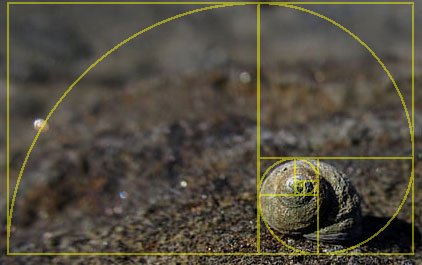
Déanann grianghrafadóirí proifisiúnta iarracht an cóimheas órga a úsáid ina bpictiúir
Má amharcaimid sa nádúr, tá go leor cosúlachtaí idir an bhís órga agus gnáthrudaí a fheicimid achan lá.
Tá an cóimheas órga nó an bhís órga le feiceáil sa nádúr fosta – amarc an sliogán seo. An comhtharlú é? (Pic le Dean Marston)
Mar sin de, ní rud í an mhata a dhéanaimid ar scoil amháin. Is rud thar a bheith suimiúil agus thar a bheith úsáideach í atá gach áit thart timpeall orainn.
Má smaoinímid níos mó faoin mhata agus faoi phatrúin agus ceangail idir rudaí, b'fhéidir go mbeadh muid ábalta an domhan a dhéanamh níos suimiúla dúinn féin – go díreach mar a rinne Fibonacci.